FFT分析とウェーブレット解析の違い

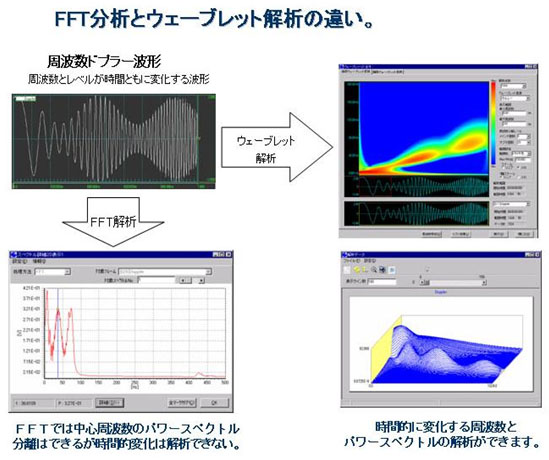
ウェーブレット解析の計算原理

周期的な運動では、少なくとも1周期以上観測しなければどのような運動かわからない、かといってあまり多くの周期について観測すると平均化されてしまう。

つまり、時間周波数の窓を通してこの運動を表す関数を見た場合、高い振動数のところでは時間を短くしなければ何周期も見ることになり、逆に低い振動数のところでは時間を長くしないと1周期分が見られない。
時間周波数の窓の面積は変えられなくても（フーリエ解析の不確定性原理：時間と周波数について同時には精度はあげられない）、その窓の形を変えることが出来るのがウェーブレット変換である。

――＞そこで、ウェーブレット変換は、その操作を行なうための関数を用いる。
ある波形からマザーウェーブレット（motherwavelet）と呼ばれている波形と相似な波形だけを抽出する。一種のフィルターのようなものです。マザーウェーブレットΨ(t)は既存のものを使用してもいいし、自分で定義して使用することもできる。

このマザーウェーブレットをスケール(伸縮）、トランスレート(平行移動）することによって、解析する波形中のこれと相似な様々なスケールの波形を、時間軸情報を失うことなく抽出することができる。以上のことを示したウェーブレット変換の定義式が次式です。

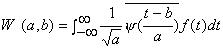
積分の範囲は、-∞から∞となっているが、マザーウェーブレットがサポートコンパクトである為、-∞から∞まで計算する必要はない。

W(a,b)は、ウェーブレット係数（以下ではＷ係数と示す）と呼ばれ、マザーウェーブレットΨ(t)との相似性の強さを示す量である。また、Ψ(t)の上の棒は複素共役であることを示している。
Ｗ係数は、自身の情報のほかにスケール情報と時間情報の２つの情報を持っているので、スケールと時間を軸に　Ｗ係数を高さとする等高線として結果を出力する。

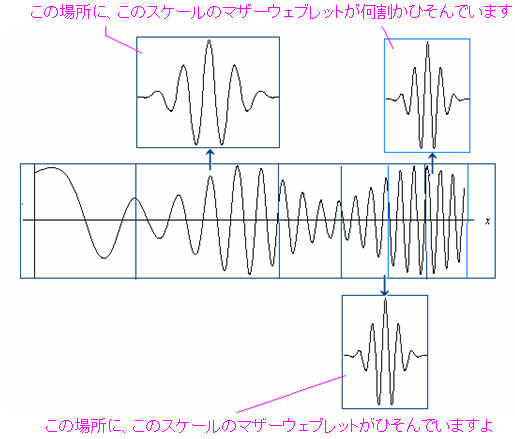
（注）スケール（伸縮）とトランスレート（平行移動）

■スケール（伸縮）
　スケールはマザーウェーブレットを横にビローンと伸ばしたり、ギュッと押し縮めたりすること。
　→　これによって、周期（周波数）を変化させることができる。
式を[ Ψ(t) → Ψ(t/a) ]とすれば、幅がａ倍され、この操作になる。

■トランスレート（平行移動）
トランスレートはマザーウェーブレットの中心位置をｔ軸上で左右に動かすこと。
　→これによって、任意の時間の相似な波形を取り出すことができる。
式を[ Ψ(t) → Ψ(tｰb) ]とすれば、中心位置がｔの正の方向にｂだけ移動する。

※マザーウェーブレットはこの２つの操作を組み合わせて使われる。
　→２つを組み合わせることで任意の時間のマザーウェーブレットと相似な波形を見つけることができる。

式を[ Ψ(t) → Ψ(t-b/a) ]にする

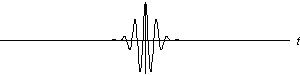
（マザーウェーブレットの例）
マザーウェーブレットの例を示します。
・モルレーのウェーブレットである。

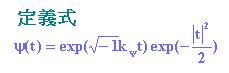
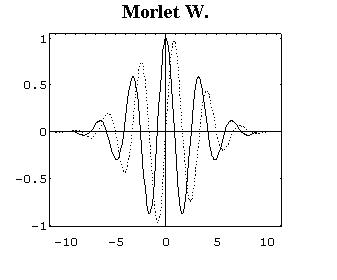
（実線は実部、点線は虚部を示している。）